PythonVoiceCodingPlugin
Sublime Text 3 plugin for voice coding Python 3
Details
Installs
- Total 2K
- Win 1K
- Mac 212
- Linux 192
| Jan 7 | Jan 6 | Jan 5 | Jan 4 | Jan 3 | Jan 2 | Jan 1 | Dec 31 | Dec 30 | Dec 29 | Dec 28 | Dec 27 | Dec 26 | Dec 25 | Dec 24 | Dec 23 | Dec 22 | Dec 21 | Dec 20 | Dec 19 | Dec 18 | Dec 17 | Dec 16 | Dec 15 | Dec 14 | Dec 13 | Dec 12 | Dec 11 | Dec 10 | Dec 9 | Dec 8 | Dec 7 | Dec 6 | Dec 5 | Dec 4 | Dec 3 | Dec 2 | Dec 1 | Nov 30 | Nov 29 | Nov 28 | Nov 27 | Nov 26 | Nov 25 | Nov 24 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Windows | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| Mac | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Linux | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Readme
- Source
- raw.githubusercontent.com
PythonVoiceCodingPlugin
WARNING : This repository will soon be deprecated as the project has been rewritten in order to support more editors Via the language Server protocol and more programming by voice frameworks. I expect a public release in October. Development will continue under the PythonVoiceCodingPlugin organization
PythonVoiceCodingPlugin is a Sublime Text 3 plugin meant in combination with the Caster toolkit to provide syntactical navigation capabilities for Python coders that are programming by voice , focusing on those who use voice input by need due to RSI/disabilities but also targeting those who simply desire an enhancement to their workflow . Users can describe what region they want to select/operate on with structured yet naturally sounding voice commands
allowing for a faster,more convenient and productive voice coding experience. The installation instructions and the 100+ gifs with examples of the documentation should help get you started and for any further questions,do not hesitate to reach out my gitter channel! With many thanks to @FichteFoll and @LexiconCode
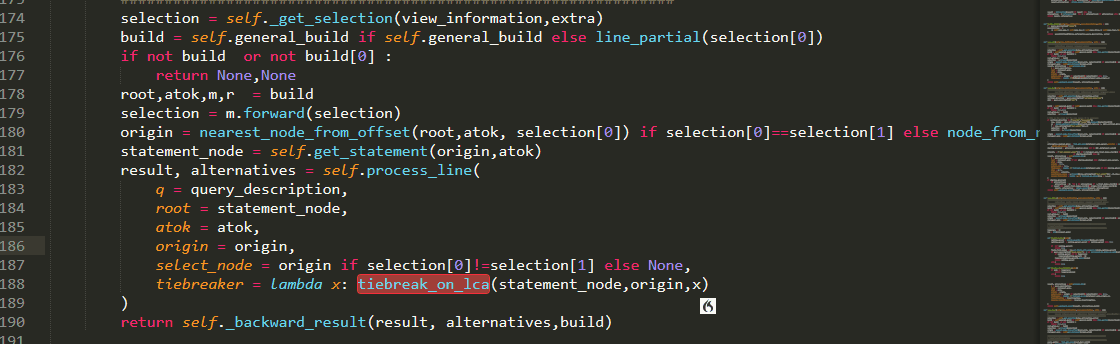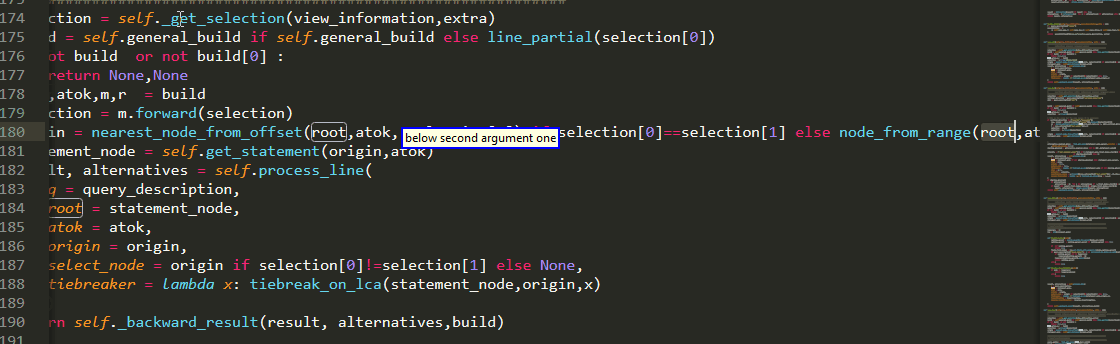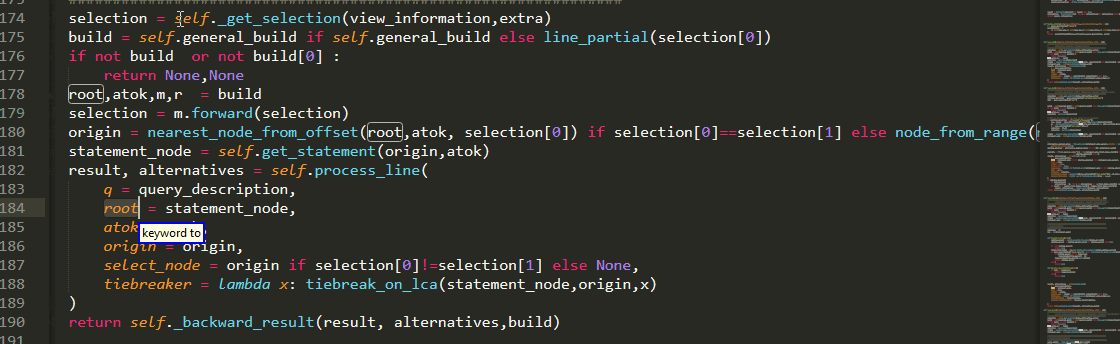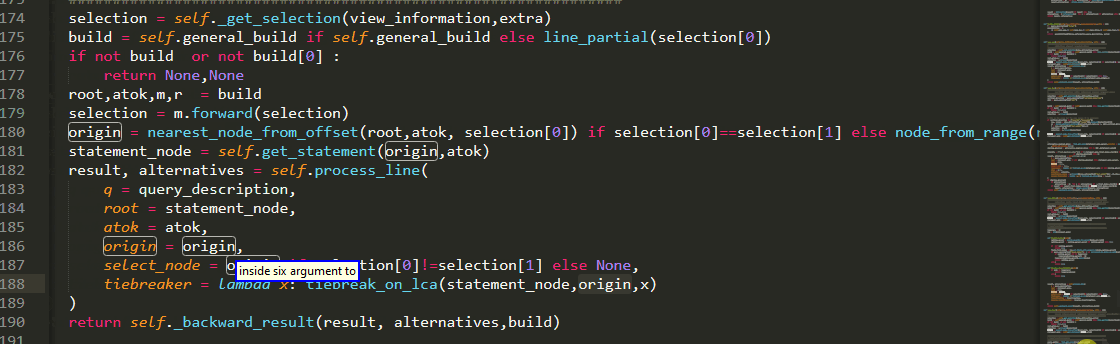
Needless to say, while coding PythonVoiceCodingPlugin , PythonVoiceCodingPlugin was and is being used :)
Contents
- Documentation
- Motivation
- Release and Version
- Limitations
- Installation
- Support for voice coding framework
- License
- Dependencies
- Acknowledgements
Documentation
Documentation is available here you can also find links to documentation under
Preferences > Package Settings > PythonVoiceCodingPlugin
Motivation
The project was inspired by Gustav Wengel's article on the state of voice coding and my personal experiences with Caster. Despite the excellent work put behind this trully awesome dragonfly based toolkit, I felt there were cases we could do slightly better:)
In particular, navigation through the code sometimes felt a little bit too mechanistic. Say for instance you want to go to some location or select some text. For the most part ,you are describing what actions need to be taken to get there. What if you could instead simply describe (syntactically) what you want to select?

PythonVoiceCodingPlugin tries to enable you to do just that! To provide this functionality, it ships with bundles the implement a grammar, hopefully expressive enough for describing regions of interest, while running on the voice coding macro system side. These bundles cooperate with the core plugin, running on the editor side, arguably the more suitable of the two environments for analyzing source code and decoding the meaning of queries within the given context.

I want to be honest. This is not exactly the best code ever written. It is far from it:) And it is far from the full functionality i would want it to offer. Nonetheless, I still think that PythonVoiceCodingPlugin is a tool that :
will give you a first taste of AST navigation of your code using abstractions such as : “smart if condition” or “below argument one”
is easy to use and learn. Commands for the most part maintain a relatively clear structural pattern and sound pretty natural.
takes a first , though addmittedly small, step towards reducing your dependency on the quality of speech recognition and your struggle with unspeakable words.
is designed on the realization that flexibility is key. I really want a lot of functionality available to you without the need to master the tool. To that end:
- the tool will go to great lengths to try and decode what you meant from incomplete or insufficient or ambiguous descriptions and suggest meaningful , color highlighted alternatives:)
- even if you fail to get what you wanted as the main result , certain operations such as paste back can work with those alternatives instead without command overhead:)
- as a side effect there are often more than one ways to select the same region so you can use whichever you think first:)
is partly customizable. If you find yourself using certain commands with some given parameters often and want a shorthand smaller command, you can always follow my commented banana example:)
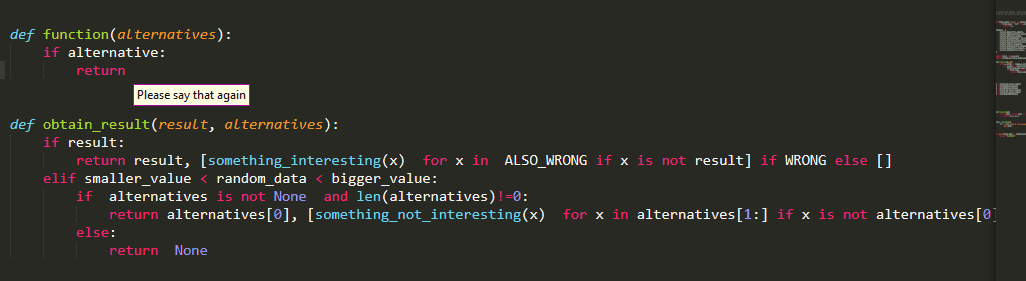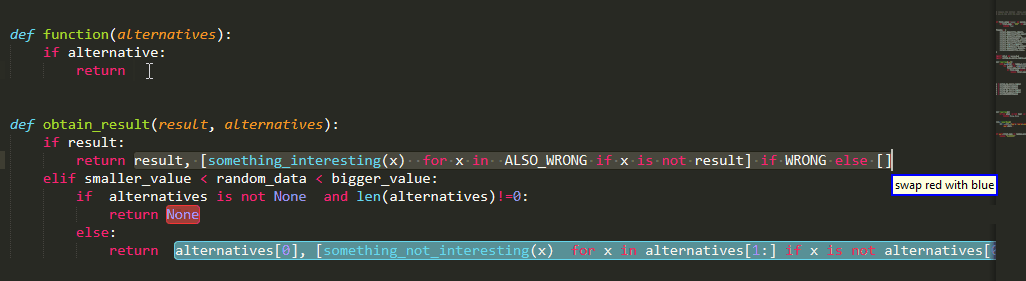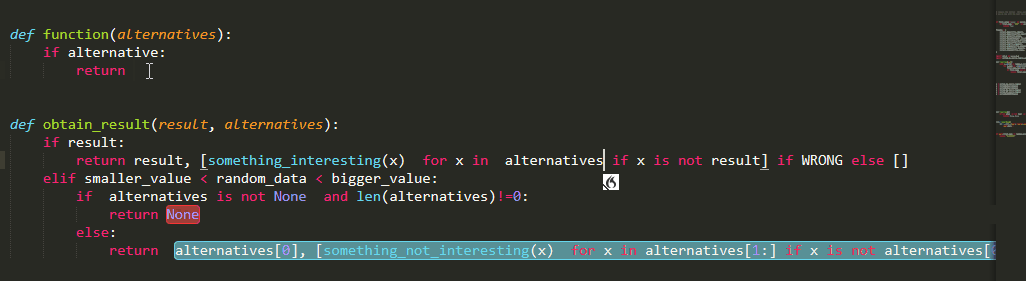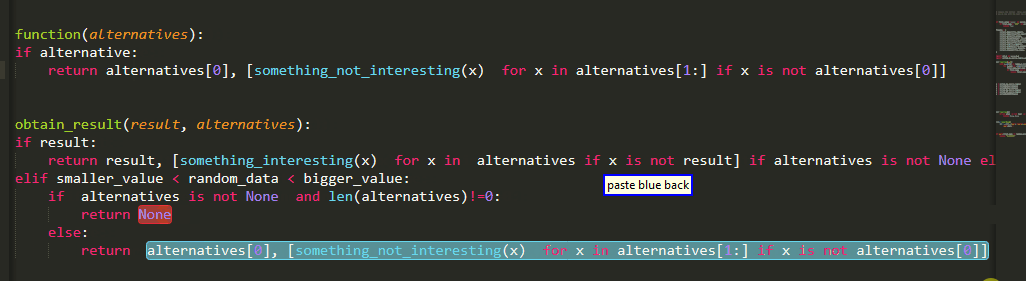
As I said, far (really far) from perfect but nonetheless an out-of-the-box solution which I hope to be helpful ,especially for beginners to get up to speed , and a step towards the right direction. I hope you enjoy using it as much as I have enjoyed coding it:)
Release and Version
The code is available on github
The latest release is 0.1.2!
Limitations
There are of course certain limitations which I would like to make clear from the start:
Currently I do not fully support python > 3.3 (Still, you can work on code that contains some new features such as async and await keywords, f-strings). That's because Sublime uses python 3.3.6 and I rely on the standard library´s ast module to parse the code. An alternative could have been astroid but it itself uses typed_ast, which contains C code, something which I wanted to avoid. The plugin will most likely eventually change to a client server architecture and simply use an up to date ast module from python 3.7 or the new 3.8. please note that this restriction only concerns the users of new syntactical features. There is no problem , for instance, if you use a new standard library function.
Furthermore, to be usable in practice it needs to be able to handle incomplete code(code where stuff is missing and thus cannot be parsed). It does so by “repairing” various common cases. Unfortunately it cannot handle everything you throw at it and in such cases most commands cannot run. Nonetheless, it can manage code like the one below:

Installation
As this is a two-part system, in order to install, you must
install the main plugin
install the corresponding grammar for the version of caster you are using
put the
sublexecutable which enables the communication of those two into the Windows path(from 0.1.2 and above optionally)
Install the main plugin
There are currently two installation (Package Control and git) methods for performing the first task,I highly recommend using Package Control.
Package Control
Firstly make sure you have Package Control installed. If not, please follow the instructions here
open Command Palette(Control+Shift+P)
execute
Package Control:Install Package
And then simply
PythonVoiceCodingPlugin
Note for those who installed between 0.0.4 and 0.0.5
previously the installation of plug-in included running
Package Control:Add Repository
and then entering a URL to my repository
https://github.com/mpourmpoulis/PythonVoiceCodingPlugin
which enabled you to install directly from a master branch rather than my releases and you should be seing a fake version like v2020.01.05.( and so on ) instead of v0.0.4.
This was only temporary solution and I recommend that you ran
Package Control:Remove Repository
so was only install/upgrade from releasees.
For the time being be warned, that the plug-in has not been tested with portable versions of sublime!
For any further installation questions, feel free to ask here
Git Install
Alternatively you can download the plugin directly from github and place it in sublime package folder
for windows users this should be:
C:\Users\Admin\AppData\Roaming\Sublime Text 3\Packages
and on Ubuntu it is : “ ~/.config/sublime-text-3/Packages/
Currently the Master Branch ships with its dependencies so you're good to go!
Just in case something is wrong and you want to manually install dependencies,using your installation of python (this worked for me with 3.7.4 and 3.5.2) run from inside the plug-in folder (PythonVoiceCodingPlugin):
```bash
python3 -m pip install --target third_party -r requirements.txt
Install Grammar
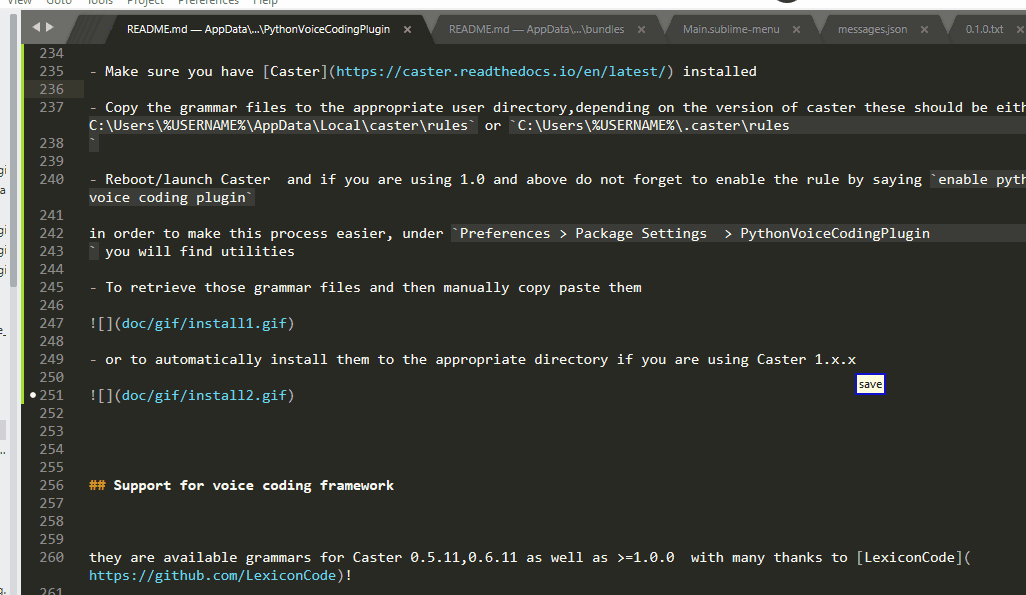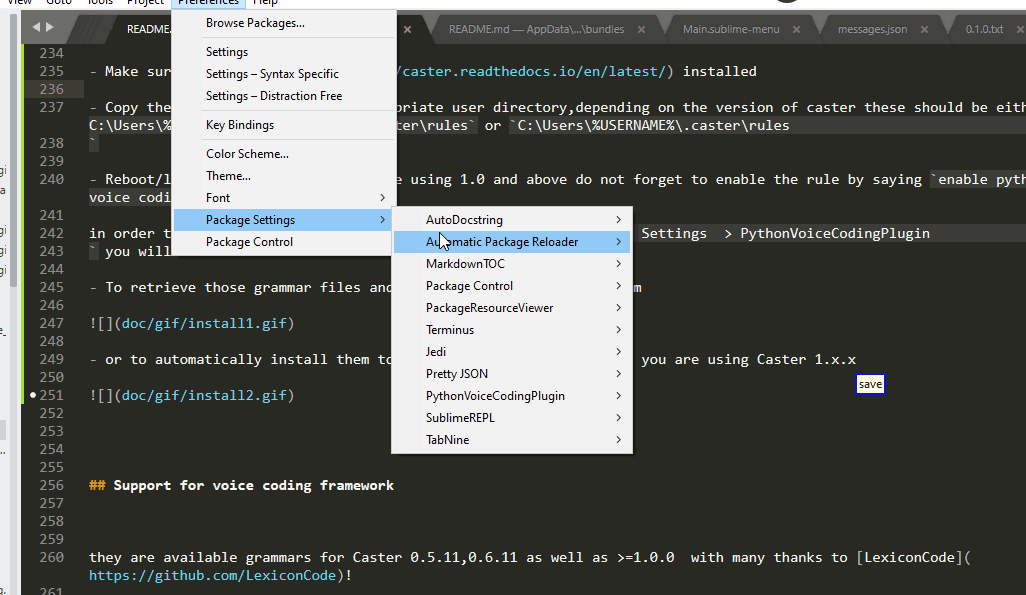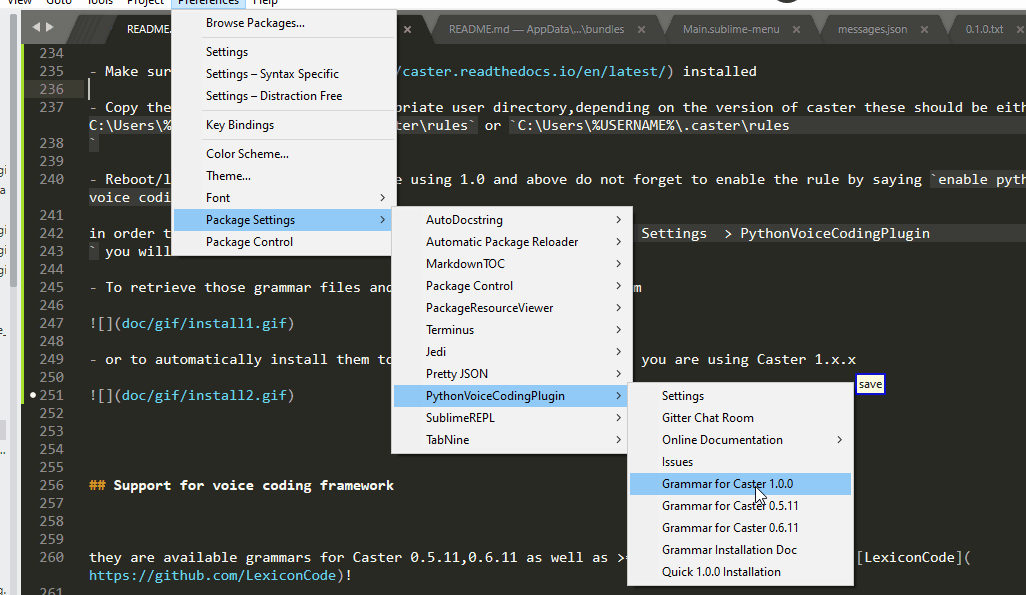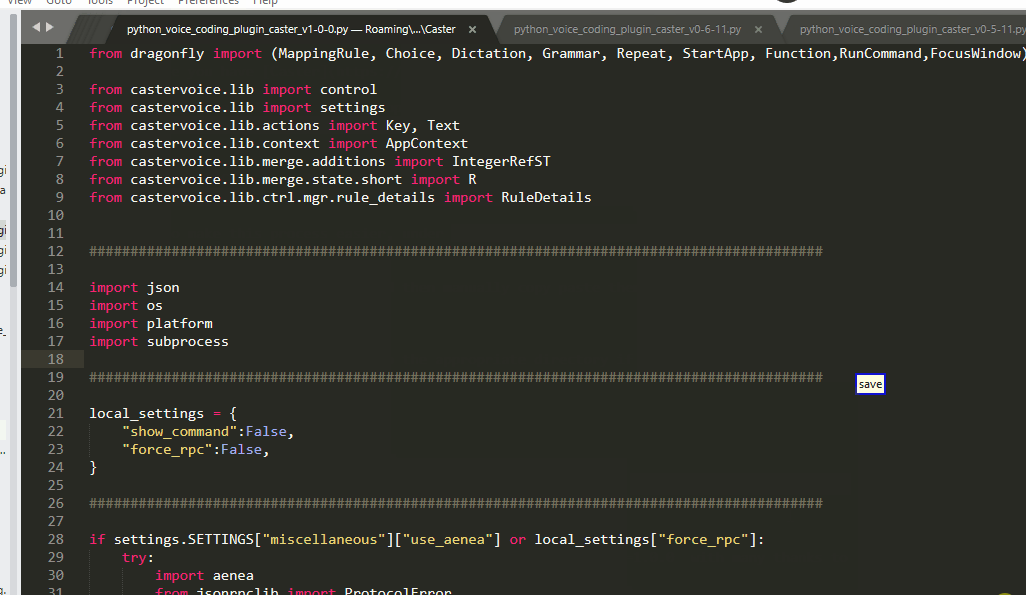
Furthermore, in order to use the plug-in, you must also install the grammar! You can find additional information here if you intend to use this on Linux via Aenea you will need a few extra steps but in a nutshell:
Make sure you have Caster installed
Copy the grammar files to the appropriate user directory,depending on the version of caster these should be either
C:\Users\%USERNAME%\AppData\Local\caster\rulesorC:\Users\%USERNAME%\.caster\rulesReboot/launch Caster and if you are using 1.0 and above do not forget to enable the rule by saying
enable python voice coding plugin
in order to make this process easier, under Preferences > Package Settings > PythonVoiceCodingPlugin
you will find utilities
- To retrieve those grammar files and then manually copy paste them
- or to automatically install them to the appropriate directory if you are using Caster 1.x.x
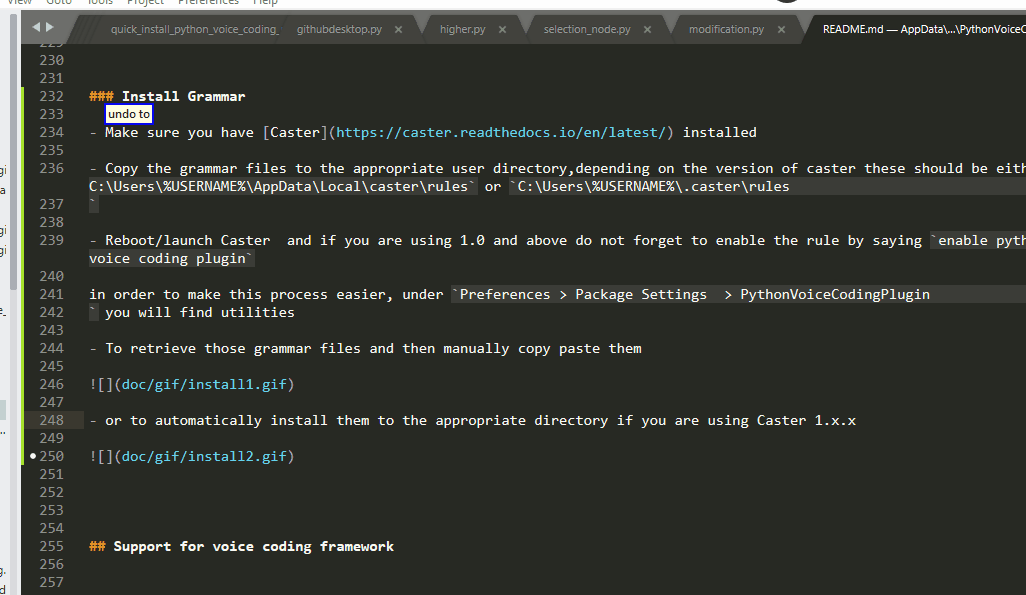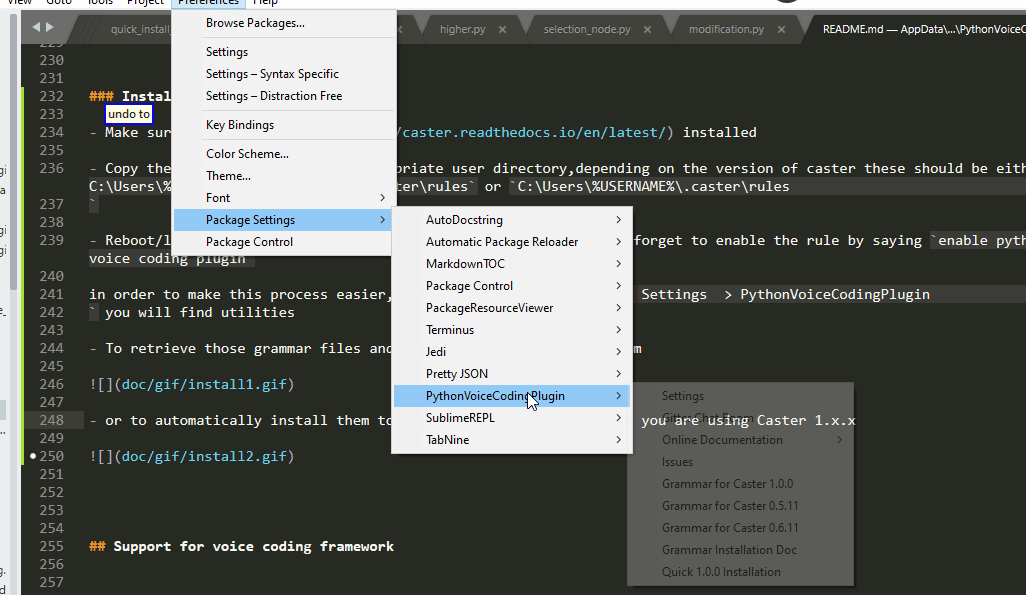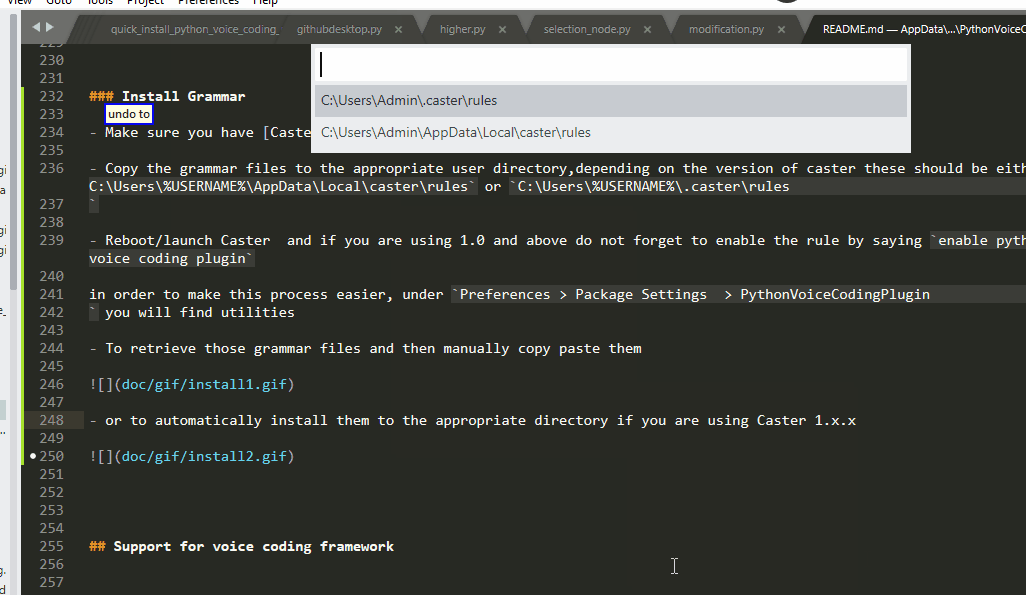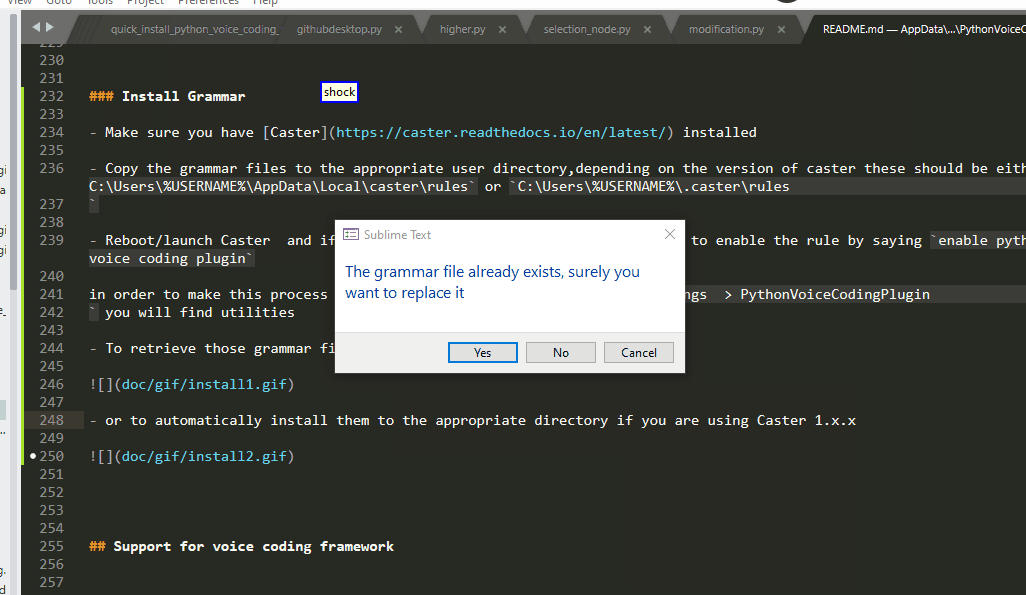
Subl Path
The communication between the main plugin and the grammar happens via the sublime command line interface through the subl executable. Up to and including version 0.1.1, it was expected that this executable is in your Windows path but as pointed out by LexiconCode the corresponding documentation was missing! these was a big blunder on my part and may have prevented you from using the project altogether!
now you can find more information about how you can add this executable to the Windows path here, but in order to work around this issue without adding an additional installation step for you, release 0.1.2 implements the following scheme:
If
sublis already in the path, it will use normallyOtherwise, it will try to fall back to
C:\Program Files\Sublime Text 3\sublwhich is where it should be if you have installed sublime in the classical way! In such a case, no extra steps are needed on your part!
if sublime is installed in another directory, you must unfortunately add it to the path yourself!
Please note that this does not affect Linux!
Support for voice coding framework
they are available grammars for Caster 0.5.11,0.6.11 as well as >=1.0.0 with many thanks to LexiconCode!
It is my highest recommendation if you are using older versions of Caster that you upgrade to the latest one. Sooner or later the plug-in is going to drop support for those older versions and either way the newer version has a lot of improvements!
Regarding operating system support, the plug-in has been tested both on Windows 10 and on Ubuntu 16.04 as release 0.0.4 introduced support for aenea!
Also note that if you are using the latest version of Caster, you must also enable the grammar by saying
enable python voice coding plugin
License
All code (grammar bundles and plugin) is licensed under 2-clause BSD License.
BSD 2-Clause License
Copyright (c) 2019, Kitsios Panagiotis
All rights reserved.
Redistribution and use in source and binary forms, with or without
modification, are permitted provided that the following conditions are met:
1. Redistributions of source code must retain the above copyright notice, this
list of conditions and the following disclaimer.
2. Redistributions in binary form must reproduce the above copyright notice,
this list of conditions and the following disclaimer in the documentation
and/or other materials provided with the distribution.
THIS SOFTWARE IS PROVIDED BY THE COPYRIGHT HOLDERS AND CONTRIBUTORS "AS IS"
AND ANY EXPRESS OR IMPLIED WARRANTIES, INCLUDING, BUT NOT LIMITED TO, THE
IMPLIED WARRANTIES OF MERCHANTABILITY AND FITNESS FOR A PARTICULAR PURPOSE ARE
DISCLAIMED. IN NO EVENT SHALL THE COPYRIGHT HOLDER OR CONTRIBUTORS BE LIABLE
FOR ANY DIRECT, INDIRECT, INCIDENTAL, SPECIAL, EXEMPLARY, OR CONSEQUENTIAL
DAMAGES (INCLUDING, BUT NOT LIMITED TO, PROCUREMENT OF SUBSTITUTE GOODS OR
SERVICES; LOSS OF USE, DATA, OR PROFITS; OR BUSINESS INTERRUPTION) HOWEVER
CAUSED AND ON ANY THEORY OF LIABILITY, WHETHER IN CONTRACT, STRICT LIABILITY,
OR TORT (INCLUDING NEGLIGENCE OR OTHERWISE) ARISING IN ANY WAY OUT OF THE USE
OF THIS SOFTWARE, EVEN IF ADVISED OF THE POSSIBILITY OF SUCH DAMAGE.
Dependencies
Many thanks to the contributors and maintainers of the following pypi packages:
For specific versions be sure to check the requirements.txt
For their licensees check out the dedicated file
Acknowledgements
Useful Learning Resources
The following resources proved to be very helpfull for the completion of the project. Many thanks to all the authors!
Green Tree Snakes an truly invaluable for this project tutorial of the python ast
sublime 3 api documentation
sublime 3 unofficial documentation
the python 3.7 grammar specification
of course the sublime forum
Development tools
Many thanks to all of the developers that have put their time and effort behind projects such as
Natlink
Dragonfly and Dragonfly2
Caster
also some of the other tools I found useful developing this project
TabNine
Quoda
Automatic Package Reloader
MarkdownTOC
ScreenToGif
Jedi
People
Last but not least many things to
LexiconCode, for porting the grammar from 0.5 to 0.6 and 1.0 versions of Caster and pointing out the missing documentation for putting the
sublutility in the path.FichteFoll, for pointing out various errors during package review







