ctrl+shift+p filters: :st2 :st3 :win :osx :linux
Browse

SAS Syntax and Theme

by Qing ST3

A Sublime Text 3 package for SAS syntax highlighting and the corresponding SAS Theme

Labels language syntax, Theme, build-system, snippets

Details

Installs

  • Total 17K
  • Win 12K
  • Mac 4K
  • Linux 1K
Jan 21 Jan 20 Jan 19 Jan 18 Jan 17 Jan 16 Jan 15 Jan 14 Jan 13 Jan 12 Jan 11 Jan 10 Jan 9 Jan 8 Jan 7 Jan 6 Jan 5 Jan 4 Jan 3 Jan 2 Jan 1 Dec 31 Dec 30 Dec 29 Dec 28 Dec 27 Dec 26 Dec 25 Dec 24 Dec 23 Dec 22 Dec 21 Dec 20 Dec 19 Dec 18 Dec 17 Dec 16 Dec 15 Dec 14 Dec 13 Dec 12 Dec 11 Dec 10 Dec 9 Dec 8 Dec 7
Windows 0 1 0 0 3 0 2 2 2 0 1 4 2 0 3 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 1 0 0 0 1 0 1 3 0 2 0 1 2 2 0 1
Mac 0 0 0 2 1 0 0 1 2 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 1 0 1 0 0 0 0 0 0 1 0 0 0 1 0 0 1 0 0 0
Linux 0 0 0 0 0 0 1 1 0 0 1 0 0 0 0 0 1 0 1 0 1 1 0 0 0 1 0 1 0 1 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 1

Readme

Source
raw.​githubusercontent.​com

SAS Syntax Highlight and Theme Package for Sublime Text 3

What is this?

A Sublime Text package for SAS syntax highlight and color scheme which mimic the SAS system.

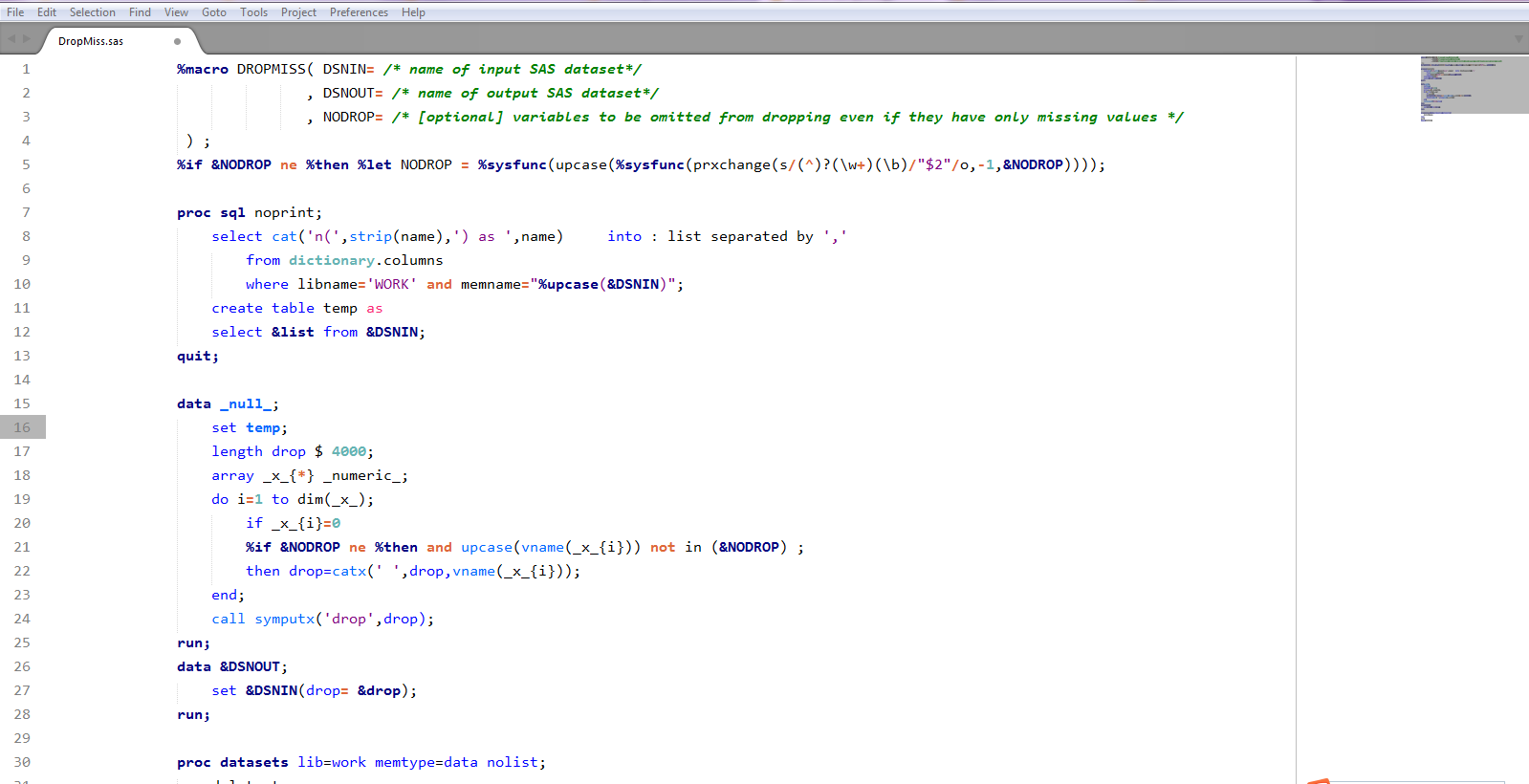
Screen Shot

How to Install

Via Package Control

The easiest way to install is using Sublime Package Control, where the package is listed as SAS-Syntax-and-Theme.

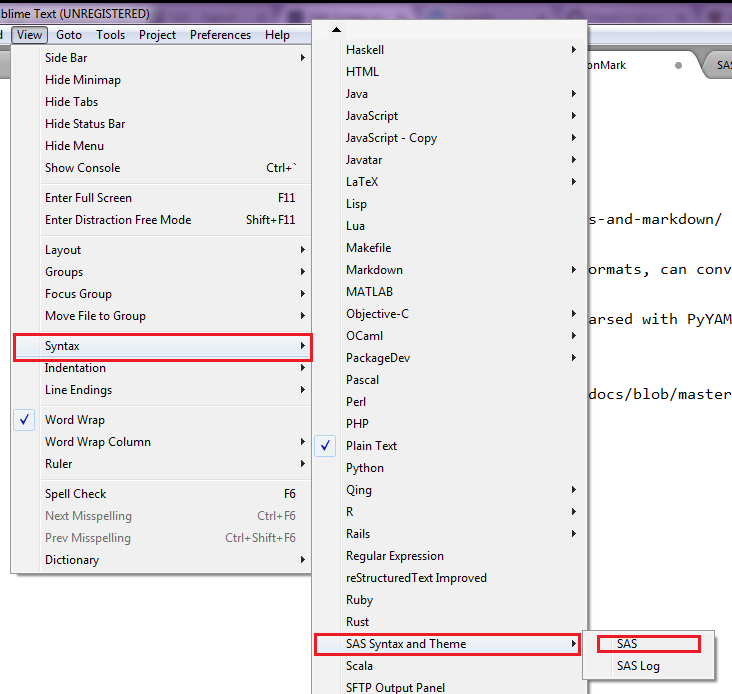
  1. Open Command Palette using menu item Tools -> Command Palette... (⇧⌘P on Mac)
  2. Choose Package Control: Install Package
  3. Find SAS Syntax and hit Enter

Manual

You can also install the theme manually:

  1. Download the .zip
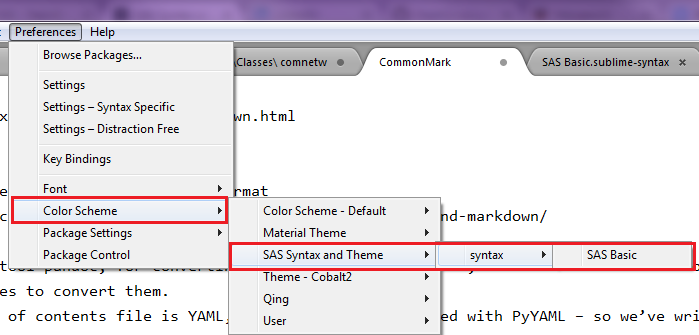
  2. Unzip and rename the folder to SAS-Syntax-and-Theme
  3. Copy the folder into Packages directory, which you can find using the menu item Sublime Text -> Preferences -> Browse Packages...

How to use

  1. Step 1: Select the SAS syntax Step 1
  2. Step 2: Select the SAS theme Step 2 ## Thanks The SAS Programming Package developed by rpardee, friedegg, seemack.